Integram theorem

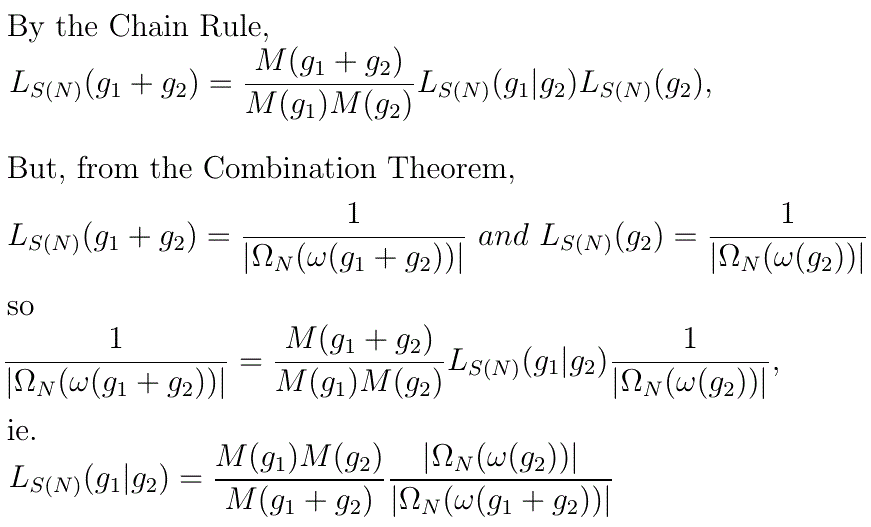
Proof

When ω(g₁)=1, this reduces to Laplace's Law of Succession. If it is required to look more than one observation ahead, it is not possible to use the Law of Succession but the Integram Theorem can be used, instead.

Example

A question, capable of being answered "Yes" or "No", is asked of 10 people. 7 reply "Yes" and 3 reply "No".

What is the Likeliness that

If one more person is asked that question then the reply will be "Yes";
If two more people are asked the question they will both reply "Yes"?

Solution

Represent "Yes" by "1" and "No" by "2". The underlying set is then S(2) and the given integram is g₂=(7,3).

Part 1. The required integram is g₁=(1,0), so we need L_S(2)((1,0)|(7,3)). We are looking only one observation ahead, so the Law of Succession may be used.

We then get L_S(2)((1,0)|(7,3))=(7+1)/(10+2)=8/12=2/3

Part 2. The required integram is g₁=(2,0), so we need L_S(2)((2,0)|(7,3)). We are looking two observations ahead, so the Law of Succession cannot be used. We shall use the Integram Theorem, instead.

We have g₁+g₂=(2,0)+(7,3)=(9,3), and so

M(g₁)=M((2,0))=(2+0)!/2!0!=2!/2!0!=1
M(g₂)=M((7,3))=(7+3)!/7!3!=10!/7!3!=120
M(g₁+g₂)=M((9,3))=(9+3)!/9!3!=12!/9!3!=220
ω(g₂)=ω((2,0))=2+0=2
ω(g₁+g₂)=ω((9,3))=9+3=12
|Ω_N(ω(g₂))|=|Ω₂(ω((7,3))|=|Ω₂(10)|=^10+2-1C_2-1=¹¹C₁=11
|Ω₂(ω(g₁+g₂))|=|Ω₂(12)|=^12+2-1C_2-1=13

Hence L_S(2)((2,0)|(7,3))=(1.120/220).(11/13)=6/13

Note that (2/3)²=4/9 (=0.4444...), not 6/13 (=0.4615...), so it would be incorrect -when answering Part 2- to use the Law of Succession (as in Part 1) and then square the result: doing so would be equivalent to assuming that the best estimate of a square is the square of the best estimate, which is the same logical trap that the Perfect Cube Factory falls prey to.