Algorithms

S(N): the set of all distributions of degree N

To find f∈S(N)

Use the computer's RANDOM function to select N-1 points in ]0,1[. These partition ]0,1[ into N subintervals. Take the lengths of those subintervals as the f(i).

Having found the f(i), as a final touch randomise them using a randomising process which is dependent upon the clock. Doing this should be unnecessary, but you never know.

R(N): the set of all ranked distributions of degree N

To find r∈R(N)

The mapping defined by

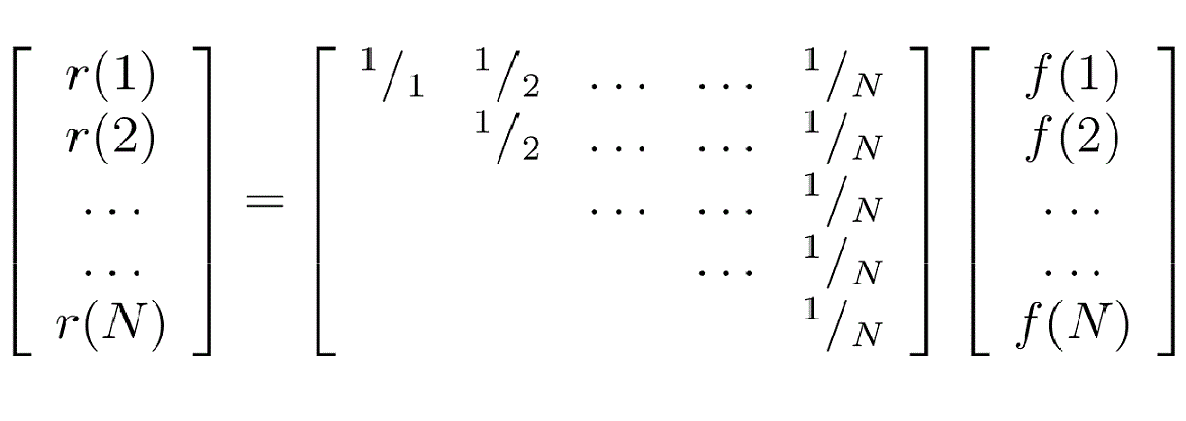
is a linear bijection from S(N) to R(N).

So, select f∈S(N) and then:-

RR(N): the set of all reverse-ranked distributions of degree N

To find f∈RR(N)

Select r∈R(N) and then, for i=1, ..., N, set f(i) = r(N+1-i).

RSD(c,N): the set of all ranked step-down distributions of degree N with step at c

To find f∈RSD(c,N)

Select r∈R(N) and randomise r(c+1), ..., r(N)

SD(c,N): the set of all step-down distributions of degree N with step at c

To find f∈SD(c,N)

Select f∈RSD(c,N) and randomise f(1), ..., f(c)

M(m,N): the set of all injective unimodal distributions with mode m, degree N

To find f∈M(m,N)

The basic idea is to start with r∈R(N)  and then permute its values to produce an element of M(m,N). We do this by firstly placing r(1), then r(2) etc.

Clearly, r(1) must be placed at m.

Since the final distribution is to be unimodal, r(2) must then be placed at either (m-1) or (m+1), since any gap would eventually give rise to a dip which would spoil the unimodality. This generalises; at each step, all of the already-placed values must form a contiguous block with the next value being placed immediately adjacent to it at either end. We need to decide which end.

At any stage, let there be L unfilled places to the left of the block and R to the right. There are then ^L+RC_L ways to choose the L values to fill the spaces to the left. In ^L+R-1C_L-1 of these, the value we are seeking to place will be to the left of the block - a proportion of  ^L+R-1C_L-1 /  ^L+RC_L , which is .

So, when deciding the end at which to place the next value, we use RANDOM to select Q∈]0,1[ and then put the next value to the left if but to the right otherwise.

M(A to B,N): the set of all injective unimodal distributions with mode between A and B inclusive and of degree N

To find f∈M(A to B,N)

There are ^N-1C_m-1 unimodal permutations of r∈R(N) which have a mode at m. So we can count the total number which have a mode at A, ..., B, and thus the proportion of those which have a mode at any specific value. We then use RANDOM to select one of them in accordance with those proportions and then construct a unimodal distribution with that specific mode.

Multimodal distributions

The description of multimodal distributions given here is actually a sufficient description of the algorithms used.

U(m,N) and U(A to B,N): U-shaped distributions

To find f∈U(m,N) and f∈U(A to B,N)

The algorithms for selecting U-shaped distributions are identical to those for unimodal distributions, except that they start with an element of RR(N) rather than of R(N).

Merge Blocks

Every time a distribution, f, is chosen, the number of observations in the merge block is pro-ratered across the columns of the block, in proportion to the f(i). These values are then added to the precise data to form the given histogram.