Lovegrove Mathematicals
"Dedicated to making Likelinesses the entity of prime interest"
Lovegrove Mathematicals
"Dedicated to making Likelinesses the entity of prime interest"
A contraction is a mapping of the form
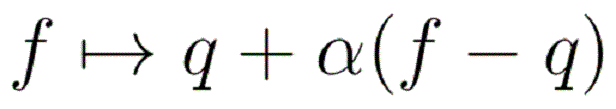
where q is a distribution which is called the centre of the contraction and α is the magnitude of the contraction.

When applied to the underlying set, a contraction might cause it to fail to be of the fundamental type originally chosen. For example, a contraction of an unimodal distribution might not be unimodal.
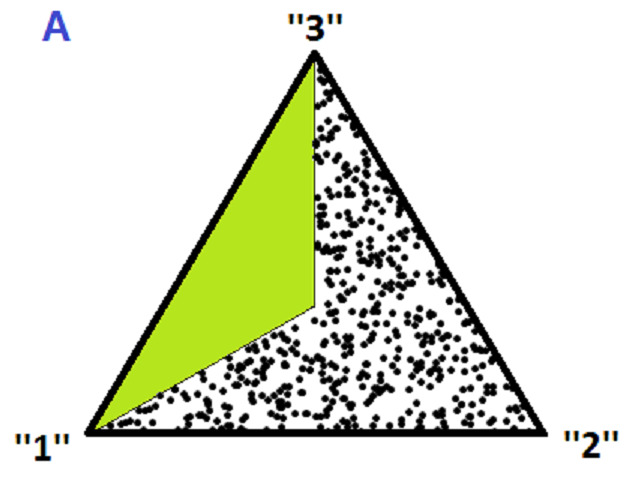
Diagram A shows S(3). The dots show M(3), ie. the unimodal distributions; the green area is the non-unimodal distributions.
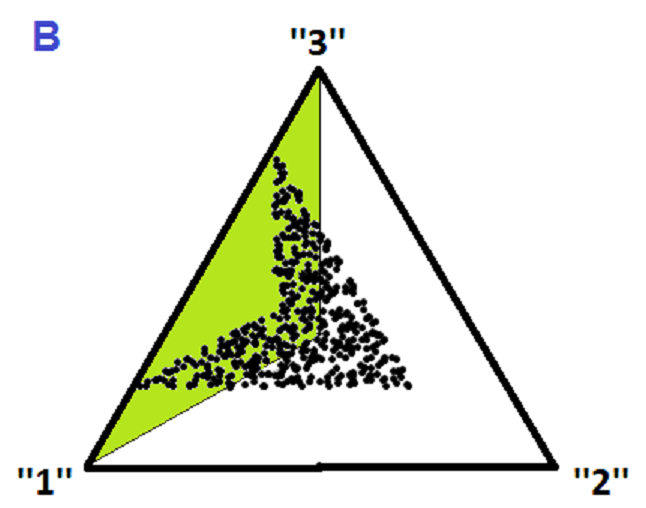
Diagram B shows the effect on M(3) of the contraction of magnitude 0.6 centred on ("1"+"3")/2. The contraction has caused about half the points which were originally in M(3) (ie. were unimodal) to move into the coloured area and so stop being unimodal.