Lovegrove Mathematicals
"Dedicated to making Likelinesses the entity of prime interest"
Lovegrove Mathematicals
"Dedicated to making Likelinesses the entity of prime interest"
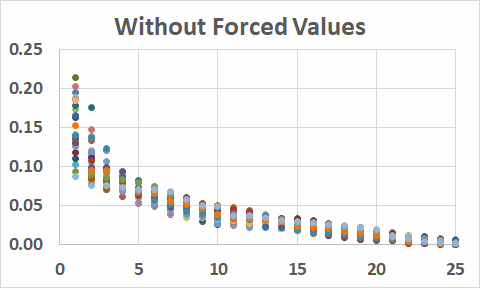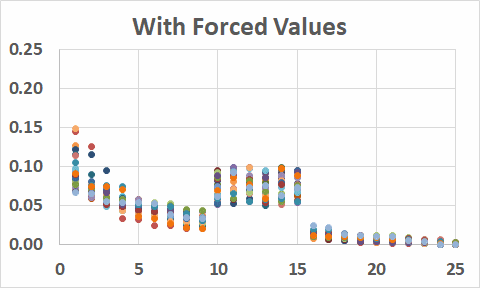
Given a set of distributions, it is not in general possible for any practical algorithm to set an interval and then select distributions which have a particular value within that interval. For example,
What we can do, however, is take a distribution and then overwrite one or more of its values with values in a specified interval. The diagram shows elements of R(25) with f(10)...f(15) overwritten by values in [0.05,0.10].
Of course, it is not just a matter of replacing one set of values by another, because that would throw out the overall sum of 1.
There are various approaches which could be taken towards algorithms for forcing values. The one I use is the simplest, but is not the most general.
The only real difficulty with any algorithm is ensuring that the overall sum remains 1. To do this, it is necessary to adjust values outside the block being forced (in the diagram, the block 10...15) to bring the sum back to 1 after the forced values have been introduced.
This means, firstly, that there must be at least one value outside that block, ie we cannot force values over the whole of the domain.
Secondly, it must be possible to bring the sum back to 1, which means that the forced values in the block must sum to less than 1. If there are n values in the block then this can be guaranteed by making each of them less than 1/n. Alternative algorithms can be devised, here, by keeping the overall sum less than 1 without requiring each individual value to be less than 1/n
The easiest way (again, there are alternatives) to bring the sum back to 1 is by simple scaling: multiply all the values outside the block by that factor which will make the sum 1 again.