Lovegrove Mathematicals

logo

"Dedicated to making Likelinesses the entity of prime interest"

Simplex of All distributions of degree N

You should read the Research Report "Fundamentals of Likelinesses", available on this website, for full details of my research into likelinesses and of likelinesses over S(N) in particular.

S(N) is the set of all distributions of degree N.

Algorithm to select f∈S(N)

Use the computer's RANDOM function to select N-1 points in ]0,1[. These partition [0,1] into N subintervals. Take the lengths of those subintervals as the f(i) [This will mean sorting the points into the correct order].

distribution from S(6)

Search the web for "sample simplex distributions" (without the quotes), or similar, for plenty of references to this algorithm. An informal explanation can be found here.

FORTRAN's pseudo-random-number generator has a period exceeding 2123. Great Likelinesses has been written to cater for the use of up to 109 distributions in a single run, with a maximum degree of about 102, giving a maximum of 1011 random number calls per run, say 1012 to allow for calls to RANDOM for other purposes, which is about 240 calls. In practice, far fewer than this will be needed because, for example, the number of distributions in a run will usually be about 106, or possibly 107, rather than 109.

Geometry of S(N)

S(N) is an open, regular (N-1)-dimensional simplex embedded in N-dimensional space. It consists of N! copies of R(N)(the set of ranked distributions of degree N) -half of which are mirror-images- together with the lines/planes etc of symmetry. Its vertices are the integrams "1", ..., "N", and its centre is the point LS(N), ie.(1/N, ..., 1/N), which is the uniform distribution.

Each of the copies of R(N) represents a permutation of R(N).

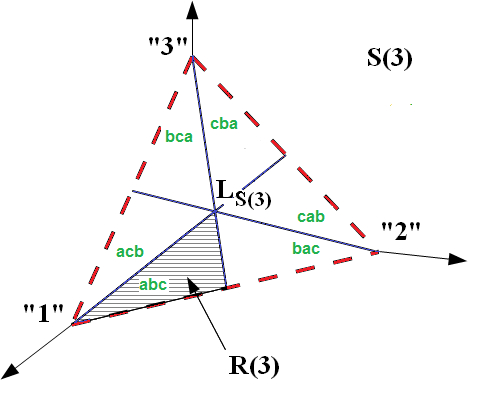
R(3) embedded in S(3)

This figure shows S(3), which is an equilateral triangle. The 3!=6 copies of R(3) are shown, and the permutations they represent are indicated by the green letters. The altitudes of the triangle separate the copies of R(3) but do not belong to any of them. They represent the non-injective elements of S(3).

Since the point abc belongs to R(3), a>b>c. So the permutations allow us to identify other underlying sets. For example, the areas acb and bca have the smallest value in the middle and so are not unimodal: M(3)(the set of injective unimodal distributions of degree 3) consists of the other four areas and can be seen (below) to be concave; its core is S(3).

Unimodal distribuutions in S(3)