Lovegrove Mathematicals
"Dedicated to making Likelinesses the entity of prime interest"
Lovegrove Mathematicals
"Dedicated to making Likelinesses the entity of prime interest"
Let f∈S(N) and c∈XN be such that [j≤c<k]⇒f(j)>f(k). Then f is a step-down distribution with step at c.
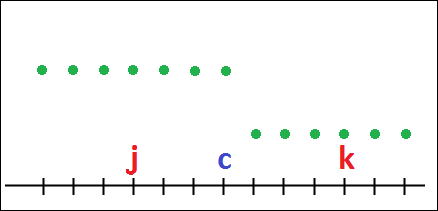
The set of all such distributions is denoted by SD(c,N).
Let f∈S(N) and c∈XN be such that [i<j≤c<k]⇒f(i)>f(j)>f(k). Then f is a ranked step-down distribution with step at c.
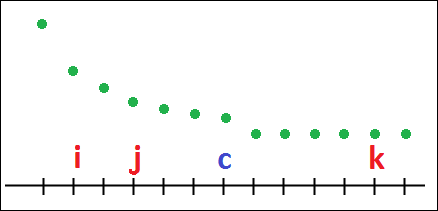
The set of all such distributions is denoted by RSD(c,N).
Every ranked distribution is a ranked step-down distribution with a step anywhere, ie. (∀c∈XN) R(N)⊂RSD(c,N)
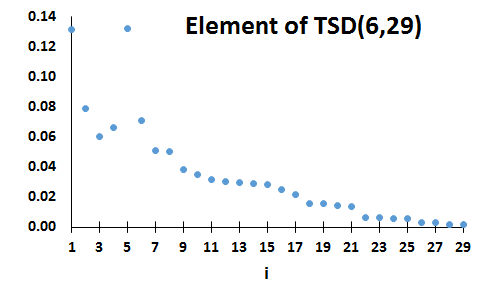
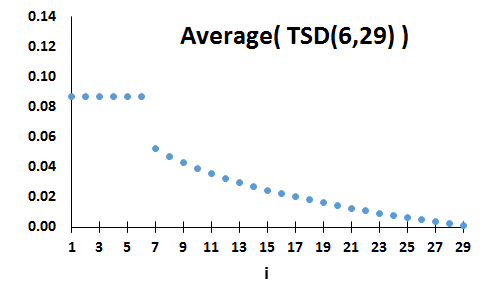
Let f∈S(N) and c∈XN be such that [i≤c<j<k]⇒f(i)>f(j)>f(k). Then f is a tailed step-down distribution with step at c.
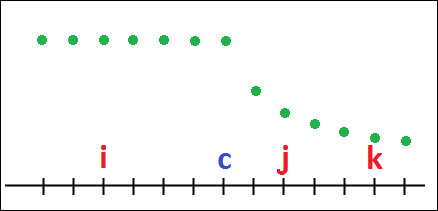
The set of all such distributions is denoted by TSD(c,N).
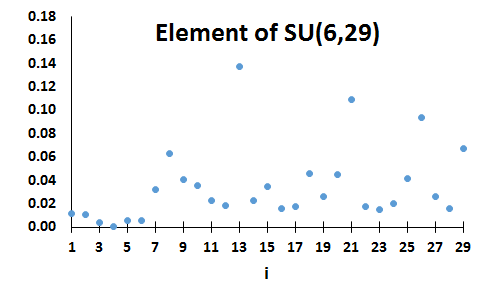
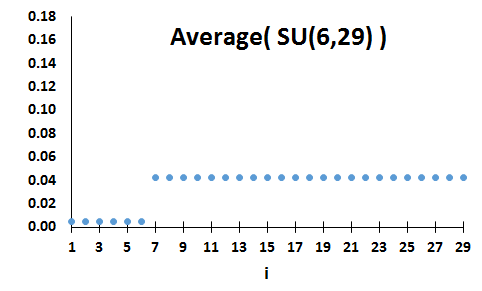
Let f∈S(N) and c∈XN be such that [j≤c<k]⇒f(j)<f(k). Then f is a Step-up distribution with step at c.
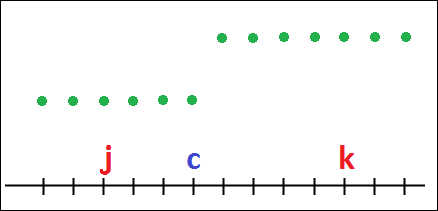
The set of all such distributions is denoted by SU(c,N).
A step-up distribution with step at c is not the mirror image of a step-down distribution with step at c. This is because of the placement of c relative to the step.
Select f∈R(N) and randomise f(1), ..., f(c) and also f(c+1),...,f(N)
Select f∈R(N) and randomise f(c+1), ..., f(N)
Select f∈R(N) and randomise f(1), ..., f(c)
It is a matter of some practical usefulness that if c=N-1 and P is any of the above sets of step-down distributions then, because f(N) is not moved by any of the randomisations, LP(N)=LR(N)(N) [=1/N2]
Select f∈RR(c,N) and randomise f(1), ..., f(c) and also f(c+1), ..., f(N)
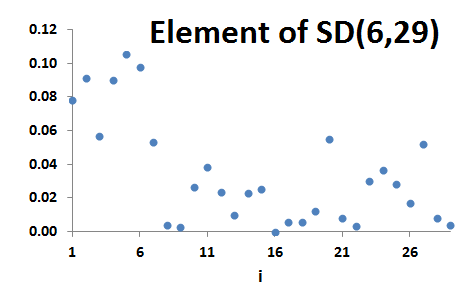
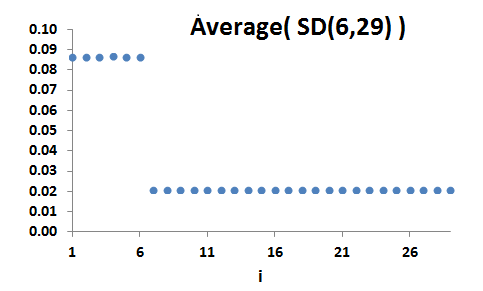
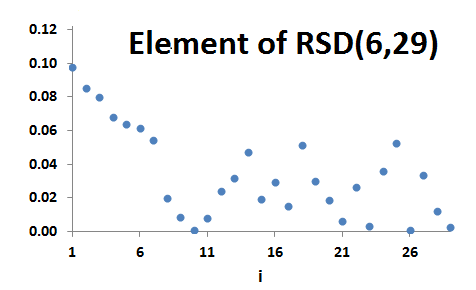
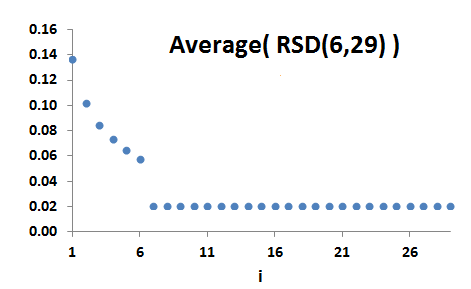
The step in a ranked step-down distribution can sometimes be interpreted as a 'limit of discrimination' for a ranked distribution: a limit beyond which it is not possible to tell the various outputs apart.