Unimodal distributions

Algorithm to find injective f∈M(m,N)

The basic idea is to start with r∈R(N)=the set of ranked distributions of degree N and then permute its values to produce an element of M(m,N). We do this by firstly placing r(1), then r(2) etc.

Clearly, r(1) must be placed at m.

Since the final distribution is to be unimodal, r(2) must then be placed at either (m-1) or (m+1), since any gap would eventually give rise to a dip which would spoil the unimodality. This generalises; at each step, all of the already-placed values must form a contiguous block with the next value being placed immediately adjacent to it at either end. We need to decide which end.

If the block extends all the way to either end of X_N then there is no decision to be made: all of the remaining values go at the other end of the block.

Otherwise, let there be L unfilled places to the left of the block and R to the right, with neither L nor R being 0. There are then ^L+RC_L ways to choose the L values to fill the spaces to the left. In ^L+R-1C_L-1 of these, the value we are seeking to place will be to the left of the block - a proportion of  ^L+R-1C_L-1 /  ^L+RC_L , which is 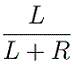: so we toss the coin 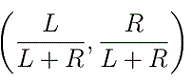. If the coin comes down "H" then we put the next value to the left; if it comes down "T" then we put the next value to the right.

Algorithm to find injective f∈M(A to B,N)

There are ^N-1C_m-1 unimodal permutations of r∈R(N) which have a mode at m. So we can count the total number which have a mode at A, ..., B, and thus the proportion of those which have a mode at any specific value. We then use RANDOM to select one of them in accordance with those proportions and then construct a unimodal distribution with that specific mode.

The shape of unimodal distributions

The general shape of an unimodal distribution as being a maxium at the mode and then dying away as we move away from the mode is a property of local modes, in particular strong local modes; it is not a property of global modes. If you have read about the meaning of 'mode' then you would have seen this.

There is a tendency for mathematical texts to give the impression that a typical unimodal distribution is bell-shaped (that is, it has tails and a rounded peak). This impression, which is far from correct regardless of whether we are using Local or Global modes, is due to the use of equations to represent distributions: there is no obvious equation for unimodal distributions which does not force a bell shape.

But being bell-shaped is such a harsh condition to satisfy that in reality it just about never occurs; certainly, there is nothing in the definition of "unimodal" which requires, or even suggests, a bell shape.

This is a random selection of elements of M(29). None of them is bell-shaped.

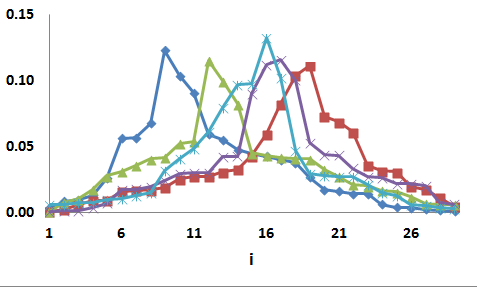
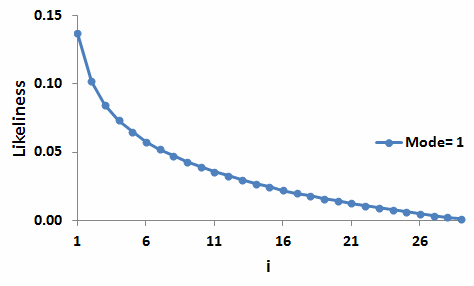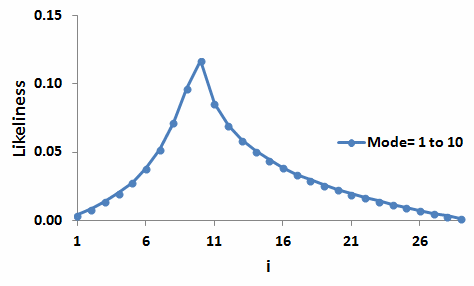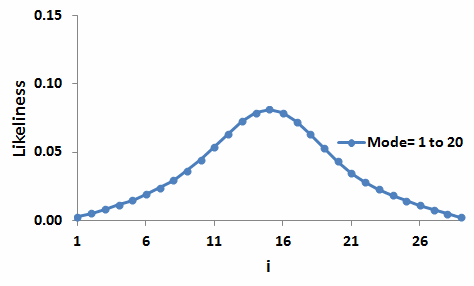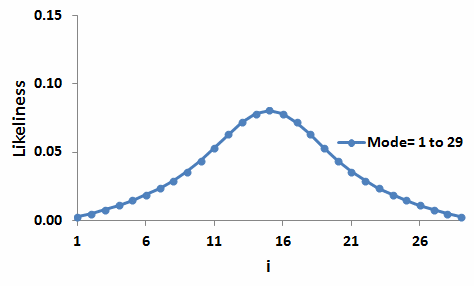
The next diagram shows the likelinesses of i=1,...,29 for distributions from the underlying set M(6,29). The graph shows what local unimodal distributions look like on average with a specific mode: the peak is very sharp, and is of a type which cannot be easily represented by a formula.

A bell shape can, however, occur on average if we do not specify a precise value for the mode.

The development of a bell shape

As we begin to allow the mode to take on a range of values, so the mean distribution begins to take on a more rounded shape. Here, with the mode allowed to vary from 3 to 10, that is with the underlying set M(3 to 10,29),we can see the beginnings of a rounding to the left of the peak.

Use of the underlying set M(1 to 13,29) brings further rounding at the peak.

With the underlying set M(1 to 16,29), the mode is ranging over most of the domain and the graph is looking almost bell-shaped.

Finally, with the underlying set M(29) a full, symmmetric bell-shape has developed.

The following animation is another way to see the development of a bell-shape as vagueness about the mode increases. Notice how the bell-shape appears to have developed once the underlying set reaches about M(1 to 21, 29), with there being no noticeable change from there on.