Lovegrove Mathematicals
"Dedicated to making Likelinesses the entity of prime interest"
Lovegrove Mathematicals
"Dedicated to making Likelinesses the entity of prime interest"
If f ∈ S(N) then m∈XN is a strong local trough of f if
By analogy with modes, there are also weak local troughs and global troughs. Global troughs are never referred to as such (simply as 'smallest value'), and we will have no interest in weak local troughs. Unless specified otherwise, a 'trough' will be a strong local trough.
The analogue to an unimodal distribution is a distribution which has precisely one trough. We could, perhaps, by analogy call these "unitroughal distributions" but we don't -we call them "U-shaped distributions". A U-shaped distribution is a distribution which has precisely one trough.
The set of all U-shaped distributions of degree N and trough m is denoted by U(m,N).
If A and B are elements of XN with B≥A then the set U(A to B,N) is defined by U(A to B,N)=U(A,N)∪U(A+1,N)∪...∪U(B,N)
If A=1 and B=N then we write U(N) rather than U(1 to N,N).
The algorithms for U-shaped distributions are identical to those for Unimodal distributions, except that they start with an element of RR(N) rather than R(N).
U-shaped distributions are identical to Unimodal distributions, except that the inequalities have been reversed.
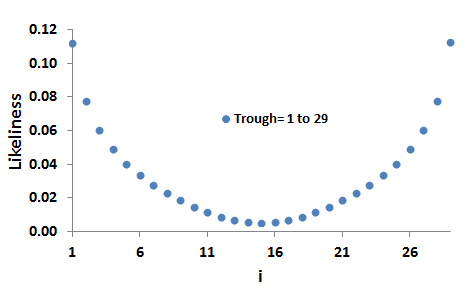
As this animation of LU(m,29)(i) demonstrates, on average the distribution is taller at the mode which is further from the trough. (Note: in this animation, the values do not actually go to zero at the trough.)

The underlying set, here, is U(29). This is the U-shaped analogue to the unimodal "bell-shaped" distribution M(29).