Reduction

S(N) Reduction

Imagine this. A computer program has been written which keeps printing the numbers 1,...,6 at random. By "at random", is meant that every time the program has to print a number it firstly selects an element of S(6) and then uses it as a generating distribution to select one of those numbers for output.

If we wanted to prevent the program outputting the numbers 5 and 6 then we could insert an IF statement immediately before the print instruction. That IF statement might say IF( (I.EQ.5).OR.(I.EQ.6) ) GOTO...  where the GOTO simply bypasses the print instruction. So the program would still produce the numbers 5 and 6 internally but not print them out.

Another way to not output 5&6 would be to select from S(4) rather than S(6); that is, not generate 5 and 6 in the first place.

Could anyone tell, by looking at the outputs (now just the numbers 1,...,4) that the program was producing 5&6 internally but not printing them out? That is, that the program was choosing by using S(6) rather than S(4)?

The answer is "No, they couldn't.".

Think in terms of symmetry. Before the IF statement had been introduced, all six numbers were being produced in a symmetrical manner which treated them all in exactly the same way. So the numbers 1,...4, in particular, were being treated symmetrically. The introduction of the IF statement does not not interfere with that symmetry, so the numbers 1,...4, are still being produced in a symmetrical way. Because they are being produced in a symmetrical way and the IF statement does not interfere with their output, they would still be output in a symmetrical way: which is what would have happened if the initial choices had been by using S(4) rather than S(6).

That process -of changing the degree by simply ignoring the unwanted terms- is what I call S(N) reduction: in this case S(4) reduction because the degree is being reduced to 4. It's a perfectly common process which seems intuitive and obvious. It is in everyday use.

R(N) reduction

Now imagine exactly the same scenario except that the initial choices of the distributions are from R(6) rather than S(6). Could someone now tell that the numbers 5&6 were being generated internally but not being printed out? That is, that the choice is being made from R(6) rather than R(4)?

The answer is "Yes, they could.".

The continual re-selection from initially S(6) but now R(6) is an averaging process, so look at what happens to the likelinesses.

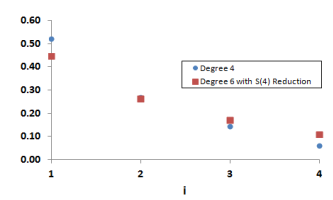
This figure compares likelinesses over R(4) with those over the S(4) reductions of R(6); they are not the same.

What's gone wrong is that we've applied S(4) reduction at the wrong stage. The selection of an element of R(N) starts by selecting an element of S(N) and then applying a linear bijection (see the algorithms) . We have applied the S(4) reduction after the linear bijection: we should have applied it before, when we had just chosen the element of S(6); if we had done that, then everything would have worked out properly.

Fortunately, if we work through the algebra then it turns out that we don't have to start messing around with linear bijections; there's a much easier way.

If we want to reduce the degree from 6 to 4, then -having selected an r from R(6)- all we have to do is subtract r(5) from each of r(1),...,r(4) and then renormalise by dividing each of them by their sum.That's R(M) reduction. For more details, see Ranked Distributions on Finite Domains.

The really important thing is that we do not have to know what the original degree was. We do not even need to know what the rest of r was, beyond r(5). For example:

i	1	2	3	4	5	6	7	...
r(i)	0.189	0.170	0.132	0.113	0.066	...	...
r(i)-r(5)	0.123	0.104	0.066	0.047
R(4) reduction	0.361	0.306	0.194	0.139

If we repeat the above Figure, but using R(4) reduction rather than S(4) reduction, we get this.

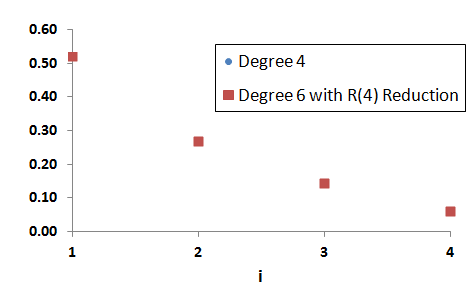
The two sets of figures coincide, so it would not be possible to tell them apart. This demonstrates that R(4) reduction can be used to generate elements of R(4) from higher-degree ranked distributions in a non-biased way.