q&A about coins and dice

Question 1

A fair coin is tossed 20 times. It comes down Heads 15 times and Tails 5 times. What is the probability of Heads? And the likeliness?

Answer

The probability of Heads is ½. Why? Because the coin is a fair coin and so is (½,½).

Since the probability is ½, the likeliness is ½. Probabilities are likelinesses.

Discussion

Probabilities are independent of the given histogram, that is of the data. The 15 Heads and 5 Tails do not affect the probabilities. Even if there had been 150 Heads and 5 Tails, the coin would still have been fair and the probability of Heads would therefore still have been ½.

Just about the only time we actually know probabilities is when they are given as part of a question, as here. We might at other times get very close to knowing them, usually when someone has gone out of their way to randomise things, such as with the Lottery, but there is always a small element of doubt.

Question 2

1. A coin is tossed once. How likely is it to come down "H"?
2. A fair coin is tossed once. How likely is it to come down "H"?
3. A coin is tossed twice. How likely is it to come down "H" both times?
4. A fair coin is tossed twice. How likely is it to come down "H" both times?
5. A coin is tossed 12 times. How likely is it to come down "H" precisely 9 times?
6. A fair coin is tossed 12 times. How likely is it to come down "H" precisely 9 times?

Answers

1. A coin is tossed once. How likely is it to come down "H"?
   By symmetry, the likeliness of "H" is ½.
   
2. A fair coin is tossed once. How likely is it to come down "H"?
   By symmetry, the likeliness of "H" is ½. Because the underlying set is singleton, we may call this the probability of "H".
3. A coin is tossed twice. How likely is it to come down "H" both times?
   There is no given data, so the given histogram is 0, and the underlying set is S(2): these meet the conditions for the Combination Theorem. The degree, N, is 2 and the sample size of the required integram, (2,0), is also 2, that is n=ω(g)=2, so |Ω_N(n)|=|Ω₂(2)|=3!/1!2!=3, so the likeliness is ⅓.
   Another way of looking at it. There are 3 possible unordered results from 2 tosses: two Heads, two Tails and one of each. By the Combination Theorem, all three are equally likely so each has a likeliness of ⅓.
4. A fair coin is tossed twice. How likely is it to come down "H" both times?
   The underlying set is {(½, ½)}; this is singleton so the Multinomial Theorem applies. So the probability of 2 Heads (and 0 Tails) is M((2,0)).(1/2)²(½)⁰= (2!/2!1!).1/4= 1/4.
5. A coin is tossed 12 times. How likely is it to come down "H" precisely 9 times?
   There is no given data, so the given histogram is 0, and the underlying set is S(2): these meet the conditions for the Combination Theorem. The degree, N, is 2 and the sample size of the required integram is 12, that is n=ω(g)=12, so |Ω_N(n)|=|Ω₂(12)|=13!/1!12!=13, so the likeliness is 1/13= 0.0769.
6. A fair coin is tossed 12 times. How likely is it to come down "H" precisely 9 times?
   The underlying set is singleton, so the Multinomial Theorem applies. The required integram is g=(9,3) so M(g)= 12!/9!3!=12.11.10/3.2.1= 220. We have f^g=(1/2)⁹(1/2)³=(1/2)¹², so the probability is Pr(g|f)=220(1/2)¹²=0.0537

Discussion

• Questions c,e. The Combination Theorem gives all integrams of the same degree and sample size the same likeliness, so there is no need to specify which one it is that we are interested in. The answer to c often comes as a shock to people who have spent a lifetime believing that the answer of 1/3 is a schoolboy error.
  
  If you feel like that then the reason is probably because you are not working from definitions, and are interpreting 'coin' as meaning 'fair coin' or 'minted coin', for which 1/3 would be naïve. In fact, 'coin' means 'any old coin'; it might be (0.99, 0.01) or (0.13,0.87), or anything else. The fact that the coin came down "H" the first time means that it's more likely than not that it is biased towards "H" (see question 3), which means that it's more likely than not that it will come down "H" on the second toss; so the answer should be greater than the fair answer of (1/2x1/2=) 1/4. The Combination Theorem takes care of the detailed arithmetic and says that the answer is 1/3.
• Questions d,f. The Multinomial Theorem, however, does need the required integram to be precisely defined.
• The appeals to Symmetry are not a matter of arm-waving and saying "it's obvious". They are references to the Theorem of Indifference (which is a theorem, not to be confused with the qualitative, and false, Principle of Indifference)
  

Question 3

A coin is tossed once. It comes down Heads. How likely is it to be biased towards Tails?

Answers

A coin is tossed once. It comes down Heads. How likely is it to be biased towards Tails?

The question is asking for the likeliness that f(2) is greater than ½ or, equivalently, that f(1) is less than ½.

In the plane, S(2) is the line joining (0,1) to (1,0). V is that part of the line to the left of its midpoint, ie. between (0,1) and (½,½). h is the histogram (1,0), and f^h=f(1). Substituting all of this into the definition of L_P(V|h) gives

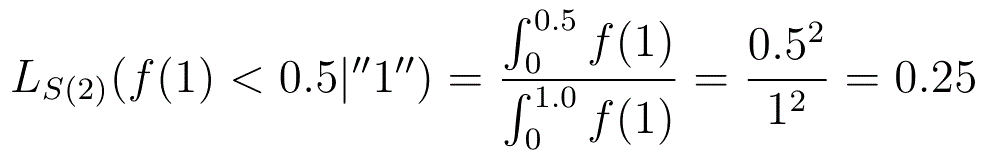
So there is a 25% chance that the coin is biased towards T, and a 75% chance that it is biased towards H.

Repeating the calculation for M tosses, all Heads, can then be seen to increase the power of f(1) inside the integrals to M. The denominator always evaluates to 1 and the power of 0.5 becomes (M+1) and hence gives the likeliness of a bias towards Tails of ½^(M+1).

Discussion

For a minted coin, a single toss of Heads would not be a strong indicator of bias towards H.

When modelling this, by using the algorithms described elsewhere on this site, with a contraction of S(2) of magnitude 0.01 and centred on the fair coin, the likeliness of bias towards Tails (given "H") is 0.4975, and of bias towards Heads is 0.5025. The effect of different magnifications is shown in the Figure.

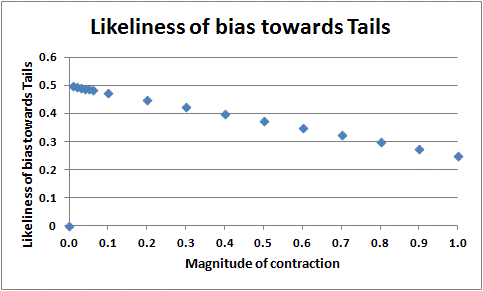
Yet, if the coin had been specified to be the fair coin then it would not be biased so the likeliness of bias towards Tails would be zero, as shown. This means that specification of the fair coin can be a degenerate case.

Question 4

A die is to be rolled 30 times. What is the likeliness that the relative frequencies after all 30 rolls will follow the uniform distribution?

The calculations are to be carried out three times:-

• Before any rolls have taken place.
• After 12 rolls have taken place and produced the results in this table

  	1	2	3	4	5	6
  Number of times rolled	3	0	2	2	3	2
  Situation after 12 rolls

• After 29 rolls have taken place and produced the results in this table

  	1	2	3	4	5	6
  Number of times rolled	4	5	5	5	5	5
  Situation after 29 rolls

Answers

The die has not been restricted to any type, such as a fair die or an actual die. It could be any die, ie any element of S(6). So the underlying set is S(6).

Case a) Before any rolls

At this stage, there have been no rolls so the given histogram is 0. The underlying set is S(6). These satisfy the conditions for the Combination Theorem.

The required integram has sample size 30 (Although it would be easy to say what the required integram is, this is not being done, just to make the point that the Combination Theorem does not need that), so we need the number of integrams of degree 6 with sample size 30, which is 35!/30!5! This is 35.34.33.32.31/5.4.3.2.1, which evaluates to 324632.

So the likeliness of obtaining any specific required integram after 30 rolls, including the one sought, is 1/324632= 3.08E-06.

Case b) After 12 rolls

The given histogram is (3,0,2,2,3,2). This is an integram and the underlying set is S(6), so the conditions for the Integram Theorem are satisfied.

Although the objective is to obtain the integram (5,5,5,5,5,5), after 12 rolls this is not the required integram. The required integram is the integram which is at that stage needed so as to give a totality equal to the objective integram: this is (2,5,3,3,2,3).

In the terms of the Integram Theorem, we have

g₁=(2,5,3,3,2,3); g₂=(3,0,2,2,3,2); (g₁+g₂)=(5,5,5,5,5,5)

We need-

• M(g₁) = 18!/2!5!3!3!2!3! = 6.17512896E+10
• M(g₂) = 12!/3!0!2!2!3!2! = 1663200
• M(g₁+g₂) = 30!/5!5!5!5!5!5! = 8.883265E+19
• |Ω_N(ω(g₂))| = |Ω₆(12)|= 17!/5!12! = 6188
• |Ω_N(ω(g₁+g₂))| = |Ω₆(30)|= 35!/5!30! = 324632

Substituting all of these into the Integram Theorem gives the required likeliness as 2.20E-05.

Case c) After 29 rolls

Again, the conditions for the Integram Theorem are being met. But there's an easier way: the Law of Succession is also applicable to this case.

This gives the likeliness as (4+1)/[(4+1)+5*(5+1)]=5/35=1/7. This is slightly less than 1/6 because the given results indicate the possibility of bias against "1".

Discussion

I also used Great Likelinesses. That gives not only the likeliness but also the Multinomial Consistency: the factor by which the Multinomial Statement would be in error if it were used regardless of whether or not the conditions for the Multinomial Theorem were being met.

Case	Likeliness	Multinomial Statement		Multinomial Consistency
a	3.08E-06	4.02E-04		7.7E-03 (=1/130)
b	2.20E-05	0.79E-06		2.78
c	0.1429	0.1429		1.0

Notice that in Case a) the Multinomial Statement would return an answer which was in error by a factor of 130 times too large.  By comparison, the error by a factor of 'only' 2.78 in case b) almost seems acceptable.